A korábbi részekből láttuk, hogy a memória táblák sorait nem IAM page-ek vagy clustered index tartja egyben, hanem egy index, amit a primary key mögé kell létrehozni. Ez lehet hash index is, de lehet egy nonclustered index is. Ezt memória tábláknál range indexeknek is szokták hívni, mivel ezzel lehet kisebb-nagyobb operátorokkal tartományokra is keresni, a hash index csak point lookupra jó.
Aki jól ismeri a nonclustered indexeket diszk tábláknál, annak azonnal beugorhat, hogy a nonclu index csak kevés sor esetén szokott hatékony lenni, sok sor esetén csak akkor, ha miden adat benne van az indexben. A fő időt a nonclustered index végéből a valódi adatokra átnavigálás viszi el, ezt hívák bookmark lookup vagy key lookupnak a planben.
Memória indexek esetén NINCS ez az overhead. Minden nclu index cover indexnek tekinthető, amint elértünk a levélszintre, azonnal “ott” van az adat. Mivel a sorok nincsenek lapokba szervezve, nincsenek page latch-ek sem.
Hogyan vannak szervezve a memória táblák nonclustered indexei?
Nyilván ez is egy fa, a normál B-Tree módosítása, Bw-Tree a neve. Aki mélységeiben akarja tanulmányozni, itt egy link az MS Research cikkhez.
A cél itt is a lock és latch mentes kialakítás volt. Az indexlapok nem fix méretűek, hanem változóak. Ha egyszer elkészült egy lap, az többé nem módosul. A hash indexeknél láttuk, hogy a lock free adatstruktúrák egyik implementációja, amikor nem módosítanak valamit, immutable az objektum, mert ahhoz szinkronizálni kellene a hozzáférést, hanem készítenek egy új példányt, majd az eredetit egy mozdulattal kicserélik az újra. Ezt az elvet használják a BwTreeben is.

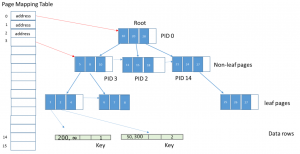
Az ábrában az a trükk, hogy az index lapok NEM egymás címét tartalmazzák, hanem a másik lap sorszámát a bal oldalon látható Page Mapping Table-ben. Azaz beraktak egy indirekciót a fa lapjainak összeláncolásába. Így már lehet azzal játszani, hogy sose módosítanak egy index lapot, hanem készítenek egy újat, és azt beláncolják a Page Mapping Table-be. Ez a már ismert CompareExchange felhasználásával.
A root lap láthatóan 3 irányba ágazik el. A 10 index kulcs alattiak a 3-as lapon lesznek, a 11-20 közöttiek a 2-esen, és a 21-28 közöttiek a 14-esen. Látható tehát, hogy minden index bejegyzés egy kulcs értéket és egy lapszámot tartalmaz, ami a következő szintre visz le.
A levélszintű lapok már közvetlenül a sorokra mutatnak. Ha egy kulcs értékhez több sor is tartozik, azok össze vannak láncolva a hash indexnél látható módon. (Diszk tábláknál a clustered indexeknél ha nem egyedi az index kulcs, akkor egy 32 bites számot generálnak mellé, hogy egyedivé váljon. Ott nincs ilyen láncolás, ezért kell ez.)

Közbenső szinten tehát úgy módosítanak egy index lapot, hogy lemásolják, módosítják, majd kicserélik a Page Mapping Table-ben a régit az új verzióra. Ez lock-free, de eléggé erőforrás igényes. Levélszinten ezt már nem lehet eljátszani, mert túl nagy lenne a költsége. Ott más trükköt használnak. Amikor módosul egy kulcsérték, akkor beraknak egy delta lapot az index lap elé. Ez a lap azt írja le, hogy az index lapon levő információt milyen módosítások értek. Az ilyen index lap picike, hisz csak egy kulcsot tartalmaz, a módosítás jellegét (insert vagy delete), illetve mutatót a “módosított” lapra.

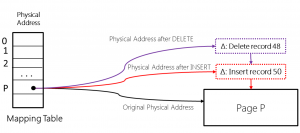
Az alábbi ábrán egy insert majd időben utána egy delete lenyomata látszik.

Először beszúrtak egy 50-es index kulcsú sort. A Page Mapping Table a művelet előtt a fekete nyíl mentén az eredeti lapra mutatott. Az insert után beláncolják az index lap elé a pirossal jelzett delta rekordot. Így összerakható az infó, hogy az index lapon látható információkon kívül még van egy új sorunk.
Ha utána törlik a 48-as kulcsú sort, akkor újra beláncolnak egy delta rekordot, ezt mutatja a lila nyúl.
Mi a poén ebben? A delta lapokat van idő összerakni, nem kell kapkodni, lockolni. Amikor kész, rámutat a következő index lapra, ami vagy egy delta page, vagy egy igazi index lap, akkor már csak egy CompareExchange, és a Page Mapping Table máris az új lapunkra mutat, beláncoltuk a listába. Ha megelőztek, semmi gond, nekifutunk még egyszer. Nyilván ezért hívják ezt optimista megközelítésnek, mert arra számítunk, kevés ütközés lesz, így megéri nekik néha újragenerálni adatstruktúrákat, jobban, mint állandóan várni a másikra.

Az update-et egy insert majd egy delete-ként valósítanak meg, az két delta rekordot eredményez.

A sok delta rekord persze jól belassítaná a műveleteket, ezért azokat gondozni kell. Ha egy művelet eredményeképpen 16-nál hosszabbá válik a delta rekord lista, akkor a változások hatását az eredeti index lapra összepakolják egy új index lapra, majd kicserélik a régi lapot az újra. A régi lapokat elviszi a Garbage Collector (erről majd későbbi részben írok, a poros sarkokkal együtt).

Ha egy lap mérete eléri a 8k-t a sok insert miatt, akkor azt kettévágják (lehetne nagyobb, nincs 8ks lapméret mint a diszktábláknál, csak kiegyensúlyozatlan lenne a fa, ha túl sok sor lenne egy lapon). Ezt két atomi CompareExchange-dzsel valósítják meg.

Ha viszont a törlések miatt a lap mérete 800 byte alá esik, vagy már csak 1 sort tartalmaz, hozzácsapják a szomszédhoz a sorait, ezt is két atomi lépésben.

Összegezve, ha nagyon gyors point lookup kell, azaz egyedi vagy nagyon jól szóró kulcs mentén kell felolvasni sorokat, akkor egy jó bucket counttal megáldott hash index lehet az optimális megoldás, mivel a hash indexnek nincs ez a módosítási overheadje.

Ha viszont tartományra kell keresni, vagy nem nagyon egyediek az értékek, akkor a range index lesz hatékony.

A következő részben a párhuzamos módosítások szervezését nézzük meg (optimistic concurrency).

Could you hire me? Contact me if you like what I’ve done in this article and think I can create value for your company with my skills.