Mielőtt tovább taglalnám a metódusokat, egy kis kiegészítés, egy kommentre válaszolva.
MI A FENÉRE JÓ EZ AZ EGÉSZ SPATIAL izé?
Nos, ha nem 1×1-es négyzetekkel dolgozunk, hanem mondjuk térképészeti adatokkal, akkor máris sok érdekes kérdést lehet megválaszolni ezekkel a lüke metódusokkal, mint például:
-Mekkora Magyarország területe?
-Melyik város van legközelebb az ország középpontjához?
-Milyen messze van egymástól a két legtávolabbi település?
-Milyen hosszú a Duna magyarországi szakasza?
-Melyik település fekszik folyóparton?
-Mekkora a vízzel borított és a száraz területek aránya egy adott részben?
-Hol van ATM automata x km-es körzetben?
Stb.
Mivel sikerült szereznem nem túl részletes, de valós adatokat Magyarországról és a szomszédokról, ezekre a kérdésekre igyekszek választ adni a későbbi részekben. Így már érthető, miért kellenek ezek a metódusok?
Geometry metódusok folytatás, előzmények itt.
Hány dimenziós az alakat? STDimensions. A pont 0, a vonal 1, a sokszög 2. Semmi meglepetés, több nem lehet, mert 2 dimenziós a koordináta-rendszerünk.
Halmazműveletek jönnek.
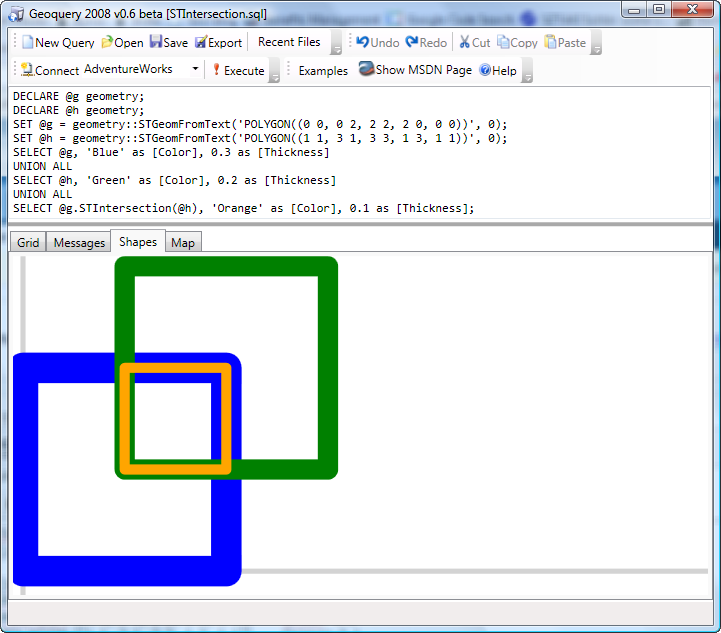
Két alakzat metszete, STIntersection.
DECLARE @g geometry;
DECLARE @h geometry;
SET @g = geometry::STGeomFromText('POLYGON((0 0, 0 2, 2 2, 2 0, 0 0))', 0);
SET @h = geometry::STGeomFromText('POLYGON((1 1, 3 1, 3 3, 1 3, 1 1))', 0);
SELECT @g, 'Blue' as [Color], 0.3 as [Thickness]
UNION ALL
SELECT @h, 'Green' as [Color], 0.2 as [Thickness]
UNION ALL
SELECT @g.STIntersection(@h), 'Orange' as [Color], 0.1 as [Thickness];
POLYGON ((0 0, 0 2, 2 2, 2 0, 0 0)) Blue 0.3 POLYGON ((1 1, 3 1, 3 3, 1 3, 1 1)) Green 0.2 POLYGON ((1 1, 2 1, 2 2, 1 2, 1 1)) Orange 0.1
A kis sárga terület a metszet.
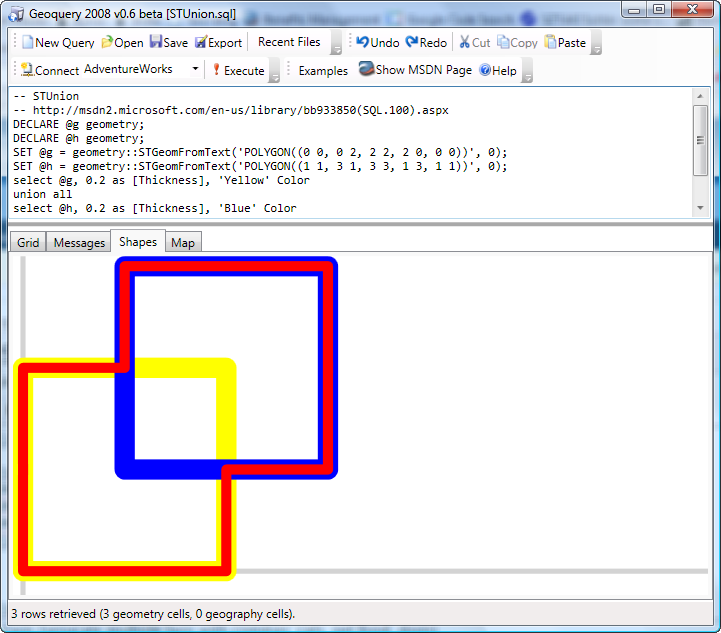
Két alakzat uniója (hogy van ez szépen, magyarul?): STUnion.
DECLARE @g geometry;
DECLARE @h geometry;
SET @g = geometry::STGeomFromText('POLYGON((0 0, 0 2, 2 2, 2 0, 0 0))', 0);
SET @h = geometry::STGeomFromText('POLYGON((1 1, 3 1, 3 3, 1 3, 1 1))', 0);
select @g, 0.2 as [Thickness], 'Yellow' Color
union all
select @h, 0.2 as [Thickness], 'Blue' Color
union all
select @g.STUnion(@h), 0.1 as [Thickness], 'Red' Color;
POLYGON ((0 0, 0 2, 2 2, 2 0, 0 0)) 0.2 Yellow POLYGON ((1 1, 3 1, 3 3, 1 3, 1 1)) 0.2 Blue POLYGON ((0 0, 2 0, 2 1, 3 1, 3 3, 1 3, 0.1 Red
Szimmetrikus különbség, STSymDifference. Az egyiket is kivonják a másikból (STDifference, láttuk már az előző részben), majd a másikat is az egyikből. Az eredő persze egy geometrikus alakzatokból álló kollekció lesz. Hogy ezt tudjuk vizualizálni, az STGeometryN metódussal beleindexelünk mindkét kollekció-elembe, és pirossal illetve naranccsal mutatom meg őket:
DECLARE @g geometry;
DECLARE @h geometry;
SET @g = geometry::STGeomFromText('POLYGON((0 0, 0 2, 2 2, 2 0, 0 0))', 0);
SET @h = geometry::STGeomFromText('POLYGON((1 1, 3 1, 3 3, 1 3, 1 1))', 0);
SELECT @g, 'Green' as [Color], 0.2 as [Thickness]
UNION ALL
SELECT @h, 'Yellow' as [Color], 0.2 as [Thickness]
UNION ALL
SELECT @g.STSymDifference(@h).STGeometryN(1), 'Red' as [Color], 0.1 as [Thickness]
UNION ALL
SELECT @g.STSymDifference(@h).STGeometryN(2), 'Orange' as [Color], 0.1 as [Thickness];
POLYGON ((0 0, 0 2, 2 2, 2 0, 0 0)) Green 0.2 POLYGON ((1 1, 3 1, 3 3, 1 3, 1 1)) Yellow 0.2 POLYGON ((2 1, 3 1, 3 3, 1 3, 1 2, 2 2, Red 0.1 POLYGON ((0 0, 2 0, 2 1, 1 1, 1 2, 0 2, Orange 0.1
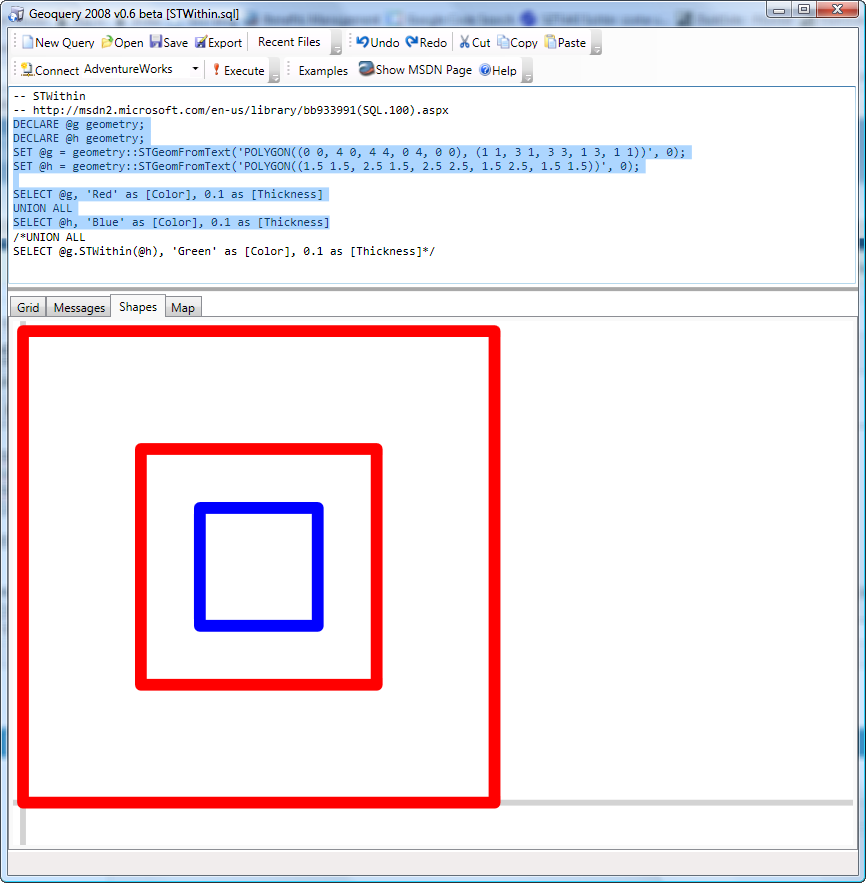
Teljesen benne van-e az egyik alakzat a másikban? STWithin.
DECLARE @g geometry;
DECLARE @h geometry;
SET @g = geometry::STGeomFromText('POLYGON((0 0, 4 0, 4 4, 0 4, 0 0), (1 1, 3 1, 3 3, 1 3, 1 1))', 0);
SET @h = geometry::STGeomFromText('POLYGON((1.5 1.5, 2.5 1.5, 2.5 2.5, 1.5 2.5, 1.5 1.5))', 0);
SELECT @g, 'Red' as [Color], 0.1 as [Thickness]
UNION ALL
SELECT @h, 'Blue' as [Color], 0.1 as [Thickness]
Ennek a kimenete false. Trükkös példát raktam össze, egy lukas négyzetet, amiben van egy másik négyzet. Persze, hogy nincs benne egyik a másikban, nemhogy részben, de egyáltalán.
Kapcsolatban áll-e két alakat? STDisjoint. Ne keverjük a jointtal. :)
Akkor Disjoint két alakzat, ha a metszetük üres halmaz.
Could you hire me? Contact me if you like what I’ve done in this article and think I can create value for your company with my skills.